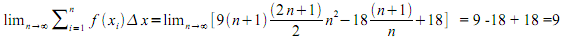Suma de Riemann
Las sumas de Riemann son un método para aproximar el área total bajo la gráfica de una curva. Llevadas al límite se obtiene la integral de Riemann.
sea f(x) una función continua en [a, b]. Sea un conjunto finito de puntos {x0, x1, x2,...xn} tales que a= x0<x1<x2...<xn = b.
consideramos la partición de este intervalo P= {[x0, x1), [x1, x2), ... [xn-1, xn]}.
Entonces la suma de Riemann de f(x) es:

Entonces la suma de Riemann de f(x) es:

donde xi-1 ≤ yi ≤ xi. La elección de yi en este intervalo suele ser arbitraria.
Si yi = xi-1 para todo i, entonces denominamos S como la suma de Riemann por la izquierda.
Si yi = xi, entonces denominamos S como la suma de Riemann por la derecha.
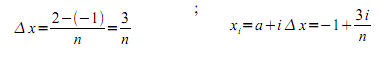
Ejemplo.
Hallar el area de la región bordeada por la gráfica de f(x)=(x-1)^2+2, en el intervalo x=-1 y X=2 mediante la busqueda del límite de la suma de Riemann.
Se divide [-1, 2]:
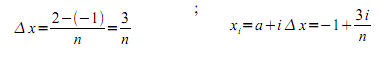
La enesima suma de Riemann es
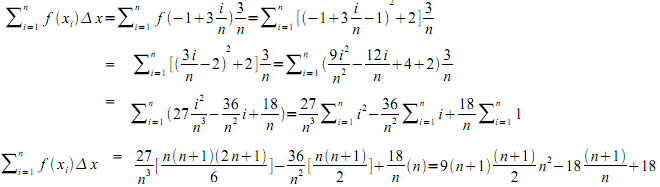
El área de la suma de Riemann: