Derivacion Parcial

Sabemos que la derivada de una función de una variable en un punto nos da la pendiente de la recta tangente a la función en ese punto. Esto significa que sabemos la rapidez de crecimiento/decrecimiento de la función en ese

punto.

Ahora supongamos que tenemos una función F que depende de más de una variable, por ejemplo

f(x,y) = -x²+2xy-y

Al ser una función de dos variables la gráfica es una superficie, y entonces hay infinitas direcciones entre las que estudiar el crecimiento.

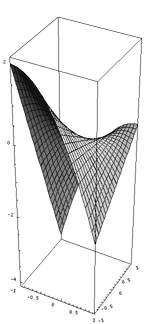
Pues bien, las derivadas parciales nos indicarán también la pendiente de una recta concreta tangente a la superficie. Antes, pero, vamos a aprender a calcular derivadas parciales, ya que es un metodologia a la que luego le daremos sentido.

Para calcular una derivada parcial de una función en diversas variables tenemos que derivar como siempre respecto una de las variables y mantener las demás como constantes, (como valores fijos).

En nuestro ejemplo f(x,y) = -x²+2xy-y , si queremos hacer la derivada parcial respecto x, consideramos la variable y como una constante, "un número", y entonces nos queda como derivar una función de una variable, f(x).

Ejemplo

-x²solo depende de x, pr lo tengt su derivada es -2x.
2xy contiene la variable y, pero es como si fuera una constante, un número. Si fuera un 3 haríamos 2x3 = 6x y la derivda seria 6. pues ahoira escribo 2xy como 2yx y considero 2y como si uera el 6. Por lo tanto la derivada de 2xy = 2yx es 2y

Y finalmente, y no contiene la variable x, y la derivaba de una constante es 0, con lo que desaparece

Asi, nuestra derivada parcial respecto x de

f(x,y) = -x + 2xy - y se escribe

d(f) = -2x + 2y -0 = 2x + 2y
d(x)

d_xf = .2x +2y

f_{x =} -2x +2y