Valor Medio
Es sencillo hallar el promedio de un conjunto de números dados, sólo debemos realizar el siguiente cálculo y prom =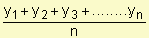 
¿Cómo calculamos la temperatura promedio durante un día si se puede tener numerosas lecturas de temperaturas? ¿Qué pasa si queremos hallar el promedio de un número infinito de valores? ¿Cómo calculamos el valor promedio de la función f(x) = x3 en el intervalo [1, 2]? ¿Cómo calculamos el promedio de cualquier función aunque no sea positiva? Estamos en presencia de un tipo de promedio "continuo".
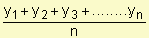¿Cómo calculamos la temperatura promedio durante un día si se puede tener numerosas lecturas de temperaturas? ¿Qué pasa si queremos hallar el promedio de un número infinito de valores? ¿Cómo calculamos el valor promedio de la función f(x) = x3 en el intervalo [1, 2]? ¿Cómo calculamos el promedio de cualquier función aunque no sea positiva? Estamos en presencia de un tipo de promedio "continuo".Se propone calcular el valor promedio de la función y = f(x), a £ x £ b. Dividimos el intervalo [a, b] en n subintervalos iguales, cada uno con longitud D x =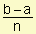
Si ti es un punto cualquiera del i-ésimo subintervalo, entonces el promedio aritmético o medio de los valores de la función en los ci viene dado por: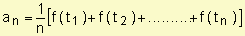
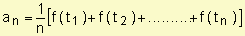
Si ti es un punto cualquiera del i-ésimo subintervalo, entonces el promedio aritmético o medio de los valores de la función en los ci viene dado por:Multiplicamos y dividimos por (b - a) y resulta:
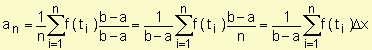
La expresión 
es una suma de Riemann para f en [a, b]. Podemos asegurar que el promedio de los n valores es 1/(b-a) veces la suma de Riemann de f en [a, b]. A medida que incrementamos la cantidad de subintervalos (D x ® 0, n ® ¥ )se obtiene, teniendo en cuenta la definición de integral definida:
es una suma de Riemann para f en [a, b]. Podemos asegurar que el promedio de los n valores es 1/(b-a) veces la suma de Riemann de f en [a, b]. A medida que incrementamos la cantidad de subintervalos (D x ® 0, n ® ¥ )se obtiene, teniendo en cuenta la definición de integral definida: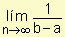
= 
= 
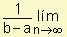
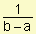
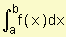
El valor promedio de f sobre el intervalo [a, b] resulta fprom =